Potential due to System of Charges

Three charges $1 \mathrm{\mu C}, 2 \mathrm{\mu C}$ and $3 \mathrm{\mu C}$ respectively are placed on the vertices of an equilateral triangle of $1000 \mathrm{m}$ side. Calculate the electric potential at the centre of the triangle.

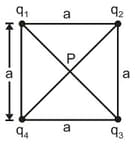
Four charges each $2 \mathrm{\mu C}$ is placed on four corners of a square of side $2\sqrt{2} \mathrm{m}$. Find the potential at the centre of square. 

A charge of $5 \mathrm{\mu C}$ is placed on each of the vertices of a regular hexagon of side $10 \mathrm{cm}$, Find the electric potential at the centre of hexagon.

Two point charges, $3\times {10}^{-8} \mathrm{C}$ and $-2\times {10}^{-8} \mathrm{C}$ are $15 \mathrm{cm}$ apart. At what points on the line joining the charges the electric potential is zero? Assume the electric potential to be zero at infinity.

Four charges, $100 \mathrm{\mu C},-50 \mathrm{\mu C},20 \mathrm{\mu C}$ and $-60 \mathrm{\mu C}$ respectively are placed on four corners of a square of edge $\sqrt{2} \mathrm{m}$. Find the electric potential at the centre of square.

For the arrangement of charges as shown in adjoining diagram, the work done in moving a  $1 \mathrm{C}$ charge from $\mathrm{P}$ to $\mathrm{Q}$ (in joule) is

Cotyledons are also called-

Assertion: When two charges are brought close to each other, potential energy of the system may increase or decrease.

Reason: When work done by a conservative force is positive, the potential energy of the system increases, and when work done by a conservative force is negative, the potential energy of the system decreases.

Assertion: The work done by a non-uniform electric field on a charged particle starting from rest may be zero. (Assume no other forces act on the charged particle).

Reason: The angle between electrostatic force and velocity of the charged particle released from rest in non-uniform electric field is always acute. (Assume no other forces act on the charged particle.)

Eight charges, each of magnitude $\mathrm{q}$ are placed at the vertices of a cube placed in vacuum. Electric potential at the centre of the cube due to this system of charges is:

( ${\mathrm{\epsilon }}_0$ is permittivity of vacuum and $a$is length of each side of the cube)

A charge $+q$ is fixed at each of the points $x=x_0,\mathrm{ }x=3x_0,\mathrm{ }x=5x_0, \dots$ upto $\mathrm{\infty }$, on $x$-axis, and charge $–q$ is fixed at each of the points $x=2x_0,\mathrm{ }x=4x_0, x=6x_0,\mathrm{ }\dots$ upto $\mathrm{\infty }$. Here, $x_0$ is a positive constant. Take the potential at a point, due to a charge $Q$ at a distance $r$ from it, to be $\frac{Q}{4\mathrm{\pi }{\epsilon }_{0}r}$. Then, the potential at the origin, due to the above system of charges, will be

An electric charge ${10}^{–3} \mathrm{\mu }\mathrm{C}$ is placed at the origin $(0,\mathrm{ }0)$. Two points $A$ and $B$ are situated at $\left(\sqrt{2}\mathrm{¸}\sqrt{2}\right)$ and $(2, 0)$ respectively. The potential difference between the points $A$ and $B$ will be

The potential at a point $P$ which is a corner of a square of the side $93 \mathrm{mm}$ with charges, $Q_1=33 \mathrm{nC}$ , $Q_2=-51 \mathrm{n}\mathrm{C}, Q_3=47\mathrm{n}\mathrm{C}$ located at the other three corners is nearly

$ABCD$ is a rectangle. At corners $B$, $C$ and $D$ of the rectangle are placed charges $+10\times {10}^{-10} \mathrm{C}$, $-20\times {10}^{-12} \mathrm{C}$ and $10\times {10}^{-12} \mathrm{C}$, respectively. Calculate the potential at the fourth corner. (The side $AB=4 \mathrm{cm}$ and $BC=3 \mathrm{cm}$)

$ABCD$ is a rectangle. At corners $B, C$ and $D$ of the rectangle are placed charges $10\times {10}^{-10} \mathrm{C}$, $-20\times {10}^{-12} \mathrm{C}$ and $10\times {10}^{-12} \mathrm{C}$, respectively. Calculate the potential at the fourth corner.

(The side, $AB=4 \mathrm{cm}$ and $BC=3 \mathrm{cm}$)

Positive and negative point charges of equal magnitude are kept at

$\left(\mathrm{0,0},\frac{a}{2}\right)\mathrm{a}\mathrm{n}\mathrm{d} \left(\mathrm{0,0},\frac{-a}{2}\right) ,$respectively. The work done by the electric field when another positive point charge is moved from $(-a,\mathrm{0,0}) to (0,a,0)$ is

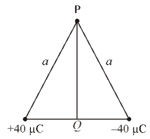
Two point charges $q_1=-10\times {10}^{-6} \mathrm{C}$ and $q_2=15\times {10}^{-6} \mathrm{C}$ are $40 \mathrm{cm}$ apart as shown in the figure. Find the potential difference between the points $P$ and $Q$.

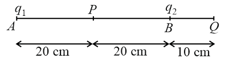
Four-point charge $q_1, q_2$ and $q_4$ are placed at the corners of the squares of side $a$, as shown in the figure. Calculate the potential at the centre of the square.


 
(Given: $q_1=1\times {10}^{-8} \mathrm{C}$, $q_2=- 2\times {10}^{-8} \mathrm{C}$, $q_3=3\times {10}^{-8} \mathrm{C}$, $q_4=2\times {10}^{-8} \mathrm{C}$ and $a=1 \mathrm{m}$.)

Two charges $+q$ and $-q$ are kept apart. Then, at any point on the right bisector of line joining the two charges,

Two point charges $-q$ and $+q$ are located at points $(0,0,-a)$ and $(0,0,a)$, respectively. The electric potential at a point $(0,0,z)$, where, $z>a$ is: